|
| ケース |
線路モデル化 |
条件 |
信号源 |
終端 |
備考 |
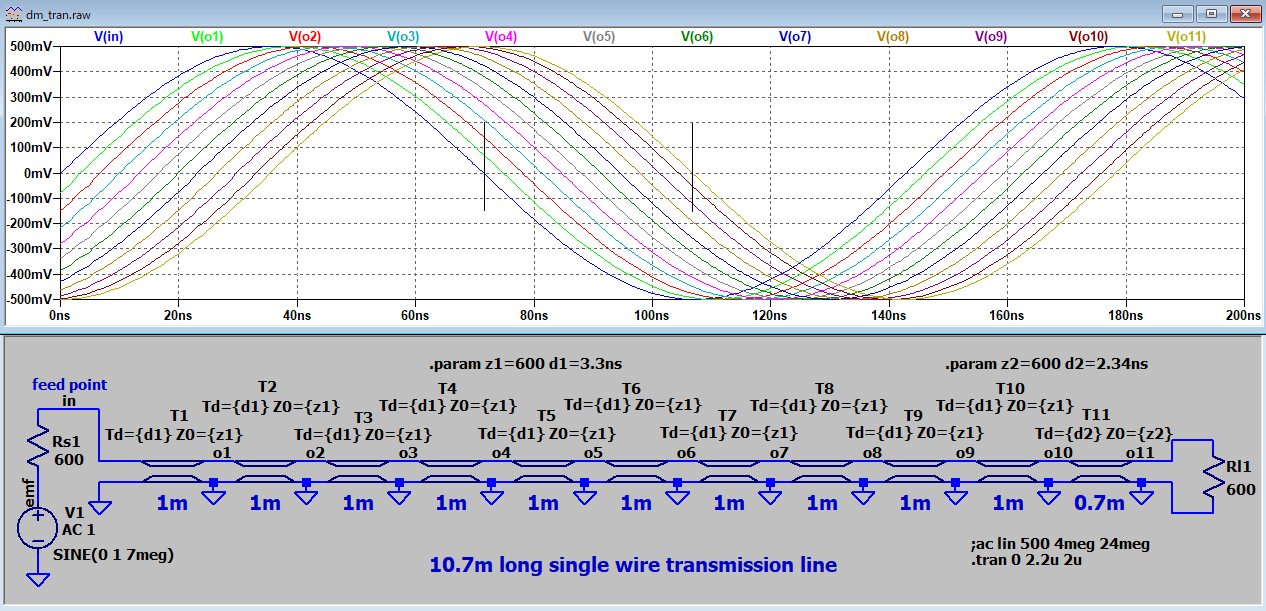
| A1 |
多段LC遅延 |
整合伝播(7MHz) |
607オーム |
607オーム |
|
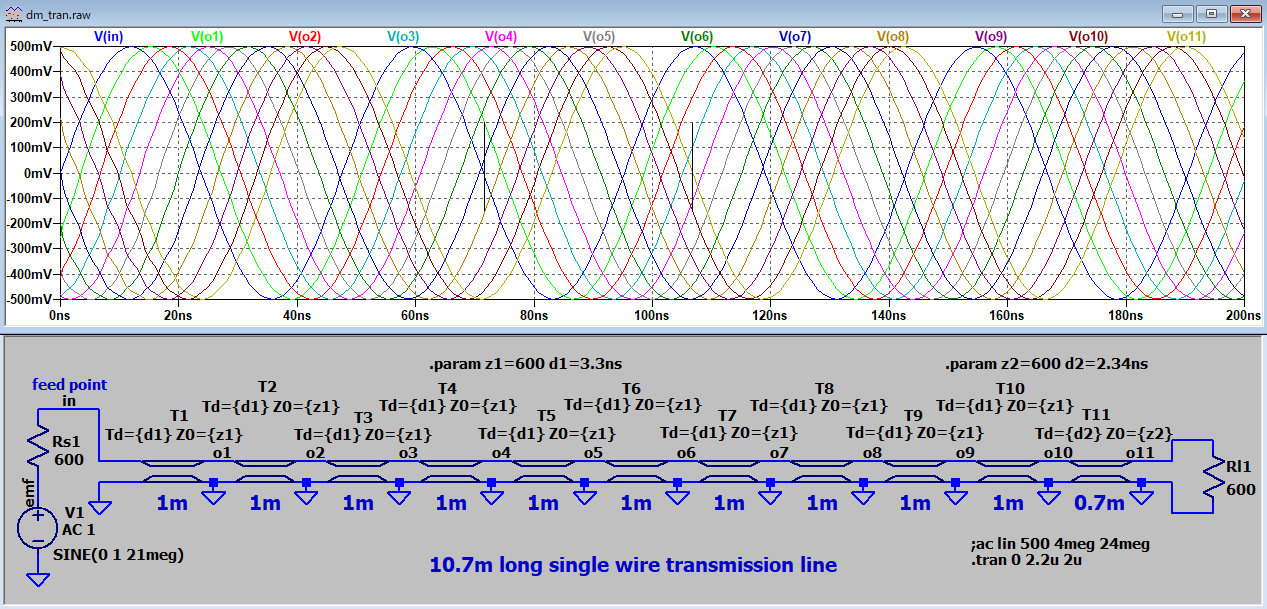
| A2 |
多段LC遅延 |
整合伝播(21MHz) |
607オーム |
607オーム |
|
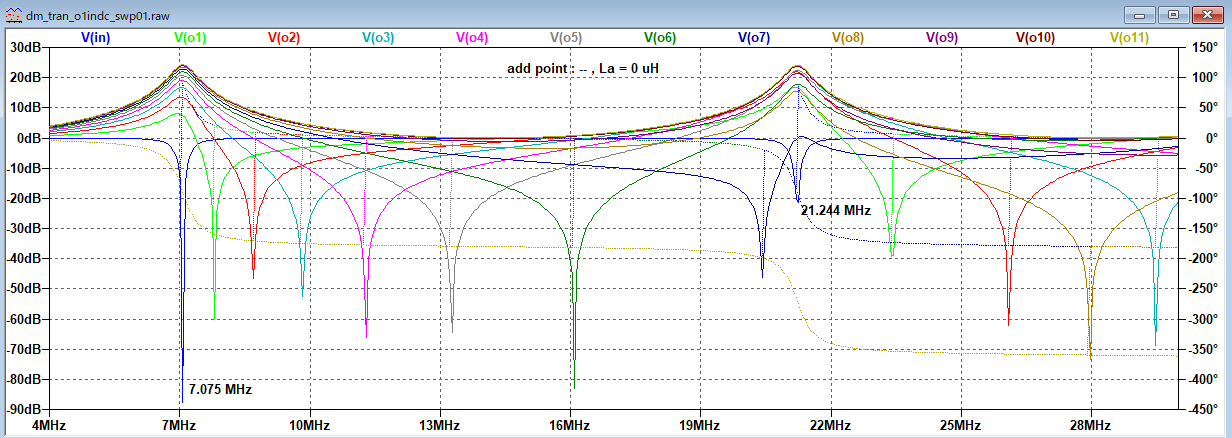
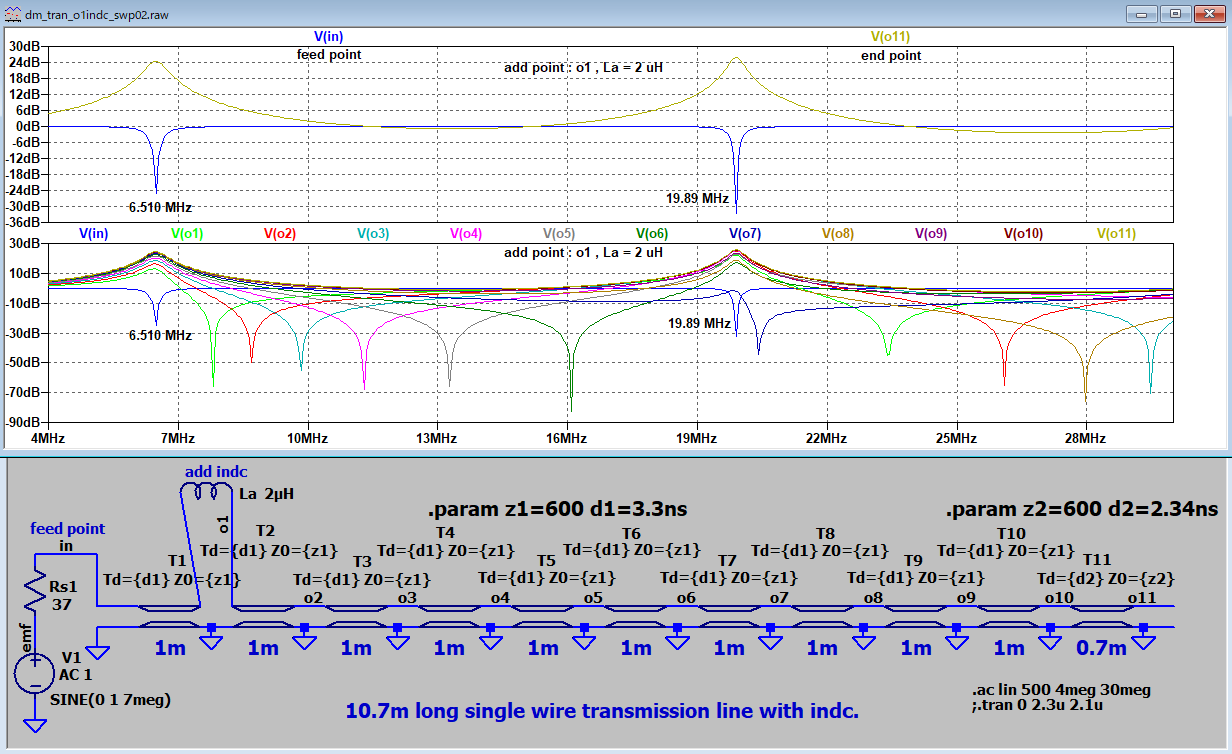
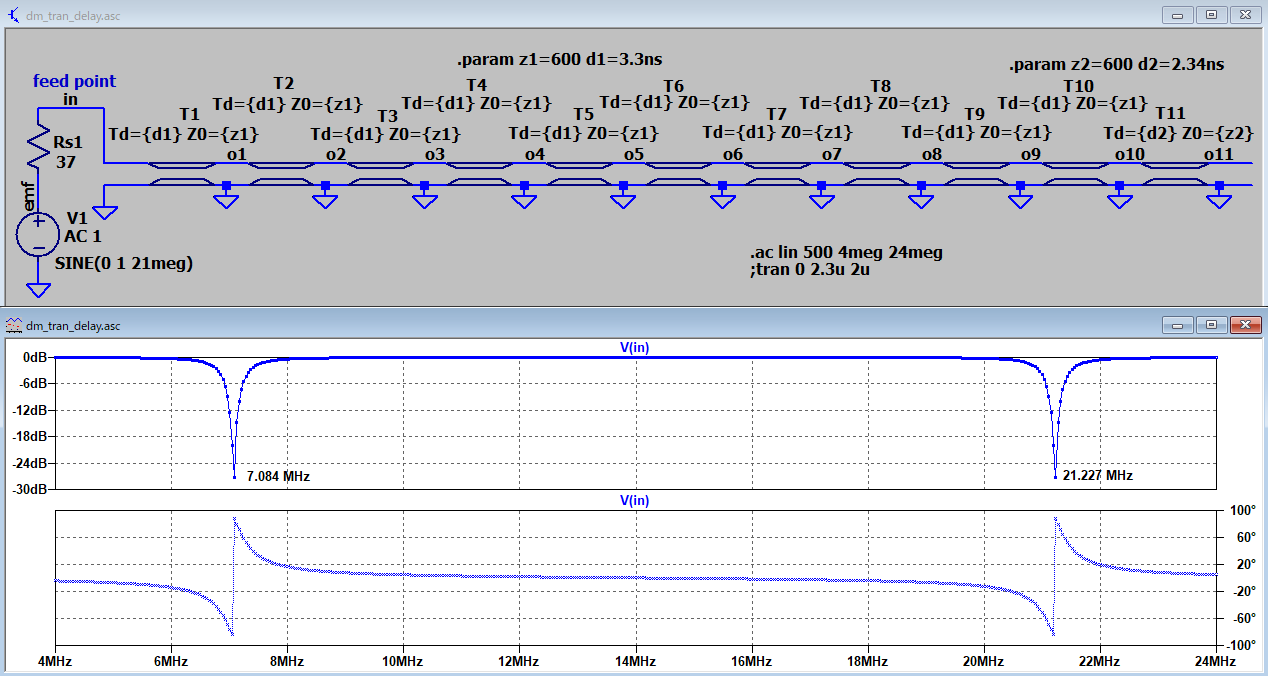
| A3 |
多段LC遅延 |
不整合伝播 共振固有値 |
37オーム |
開放 |
|
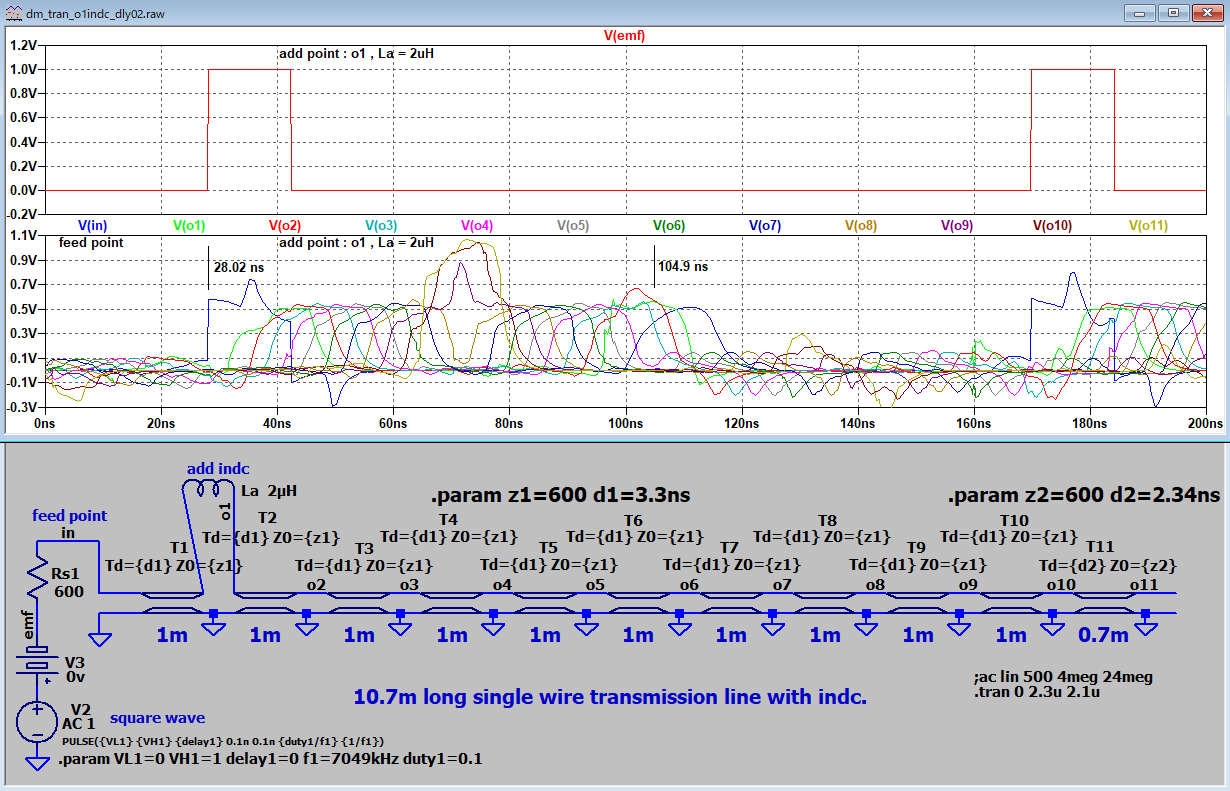
| A4 |
多段LC遅延 |
不整合伝播 反射の可視化 |
37オーム |
開放 |
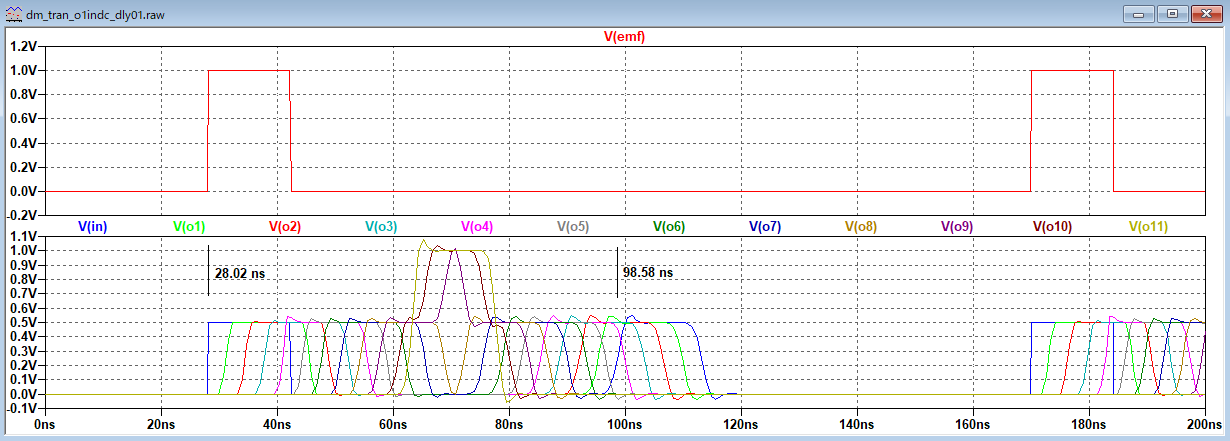
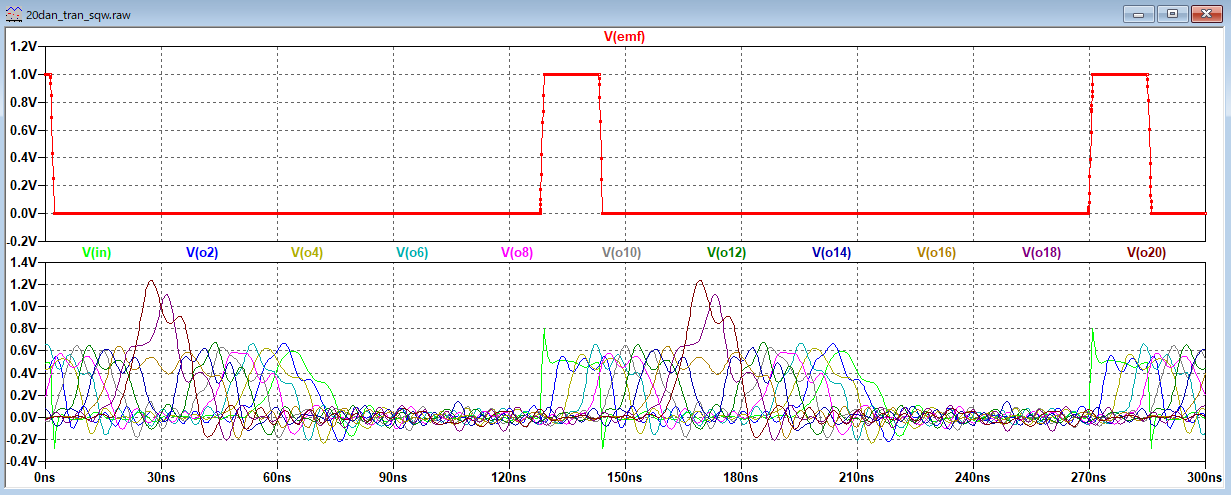
矩形波信号源 |
| A5 |
多段LC遅延 |
不整合伝播 反射の可視化 |
600オーム |
開放 |
矩形波信号源 |
| B1 |
機能演算モジュール |
整合伝播(7MHz) |
600オーム |
600オーム |
|
| B2 |
機能演算モジュール |
整合伝播(21MHz) |
600オーム |
600オーム |
|
| B3 |
機能演算モジュール |
不整合伝播 共振固有値 |
37オーム |
開放 |
|
| B4 |
機能演算モジュール |
不整合伝播 反射の可視化 |
37オーム |
開放 |
矩形波信号源 |
| B5 |
機能演算モジュール |
不整合伝播 反射の可視化 |
600オーム |
開放 |
矩形波信号源 |
|
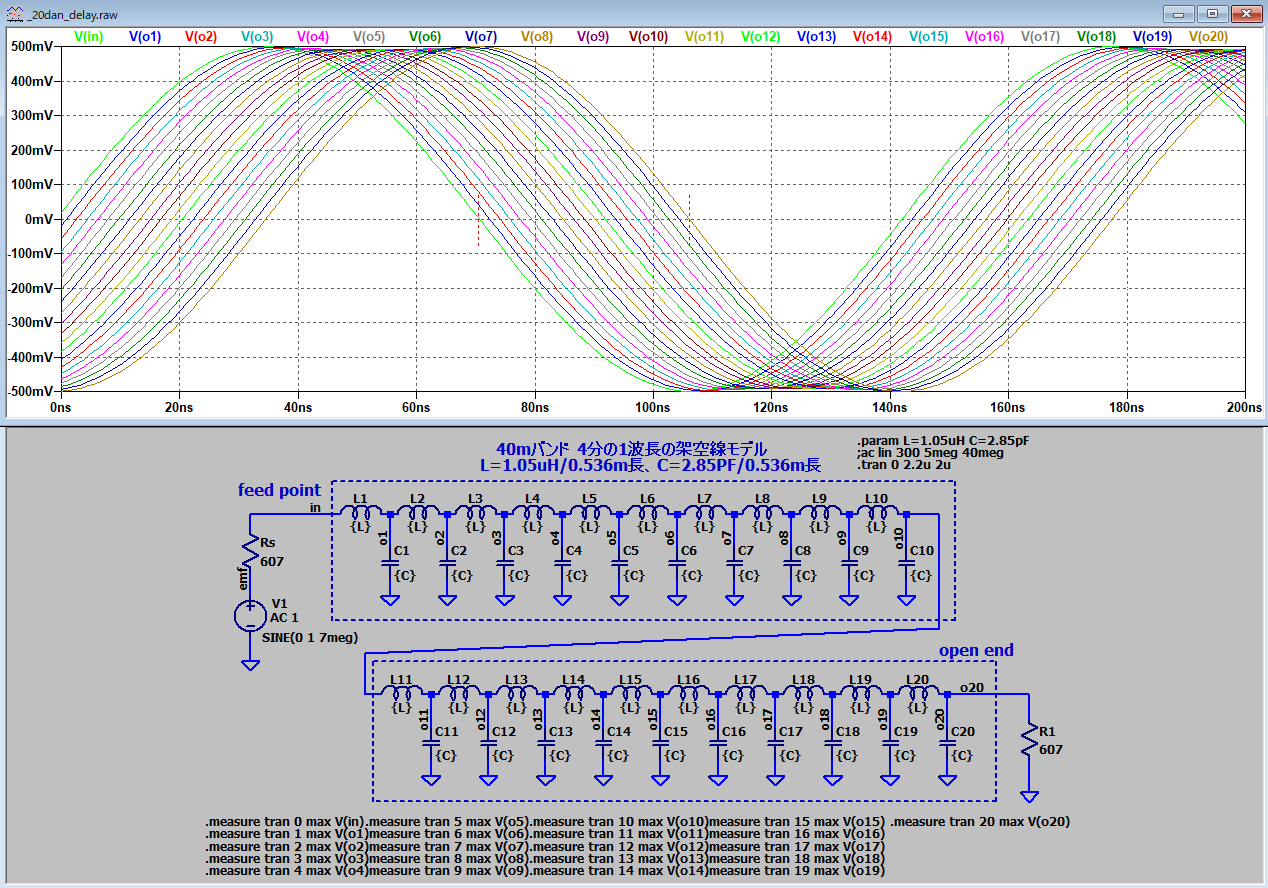
 伝送線路モデルの記述方法
伝送線路モデルの記述方法
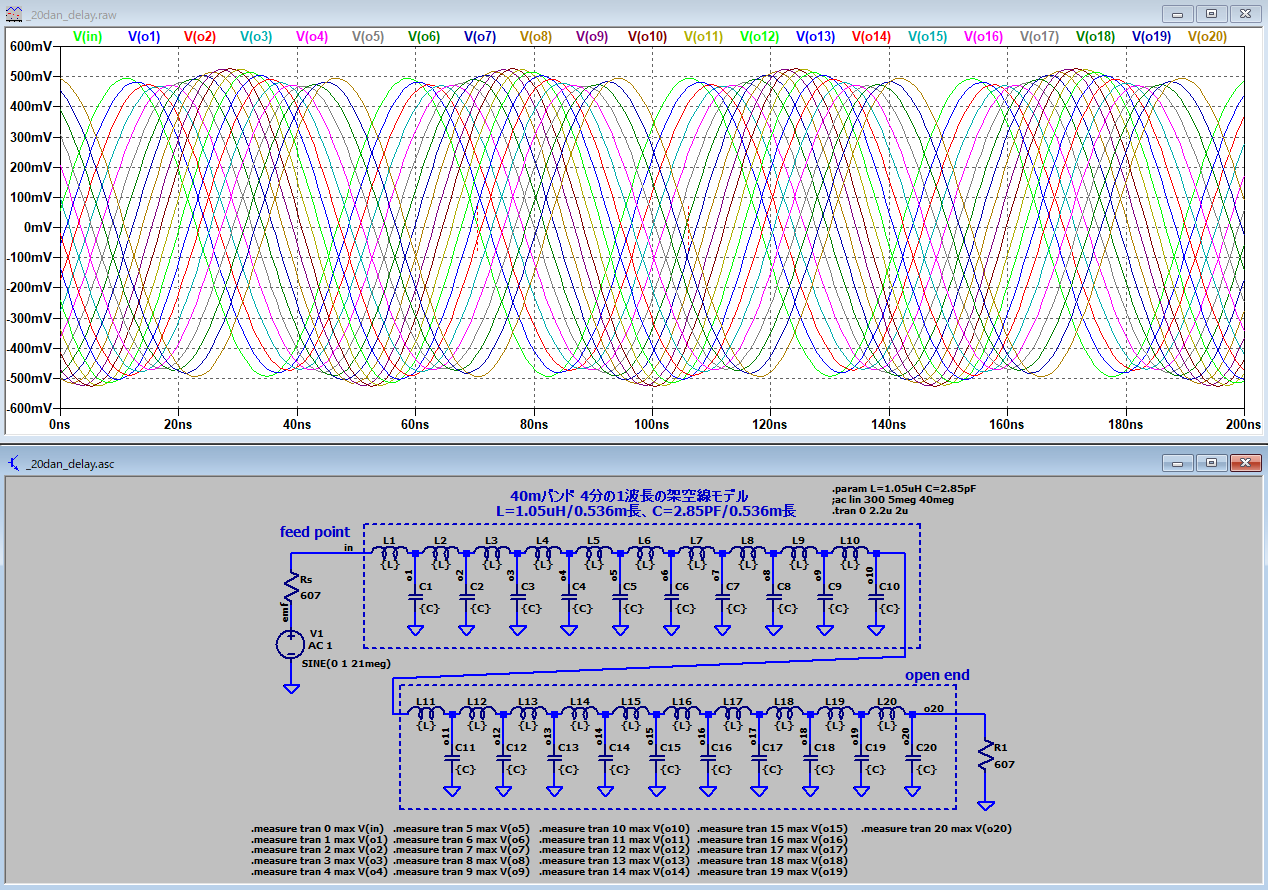
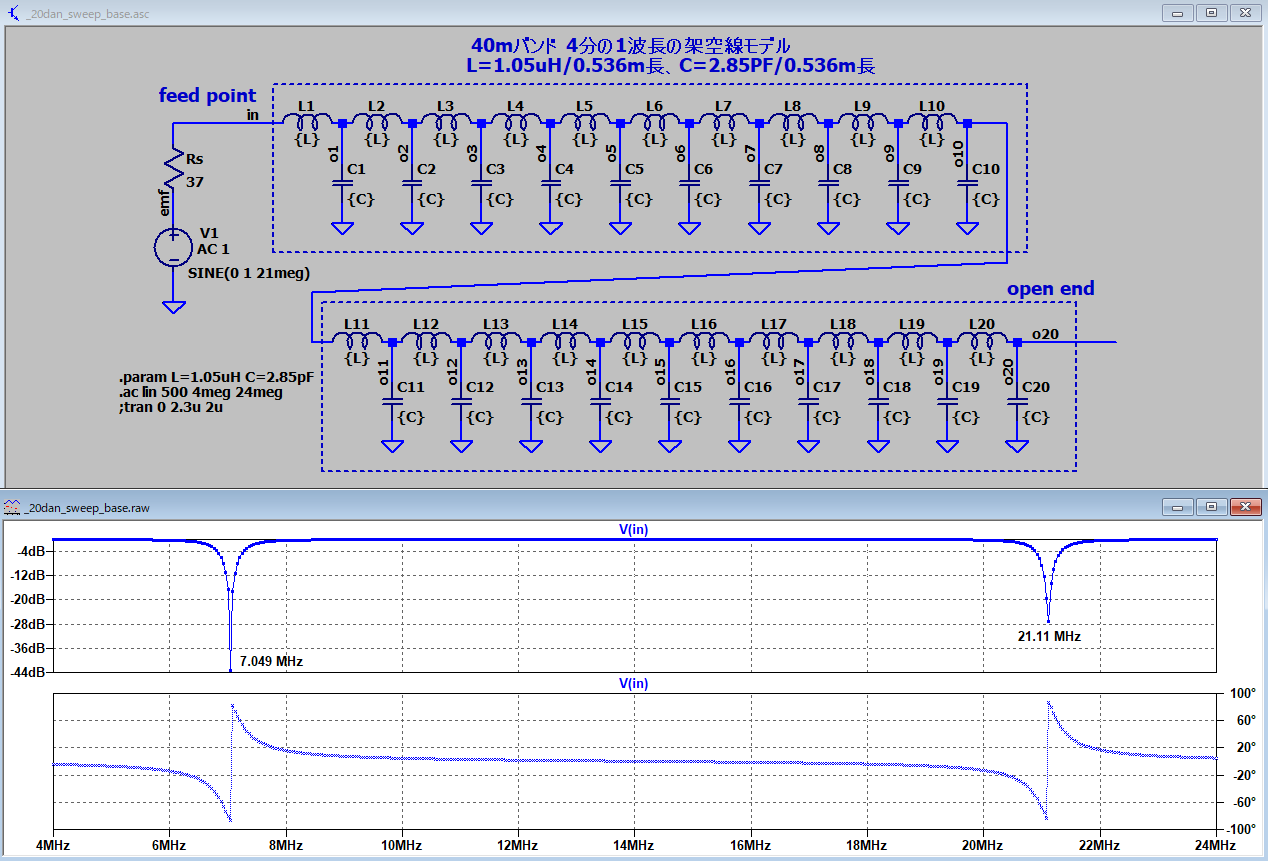
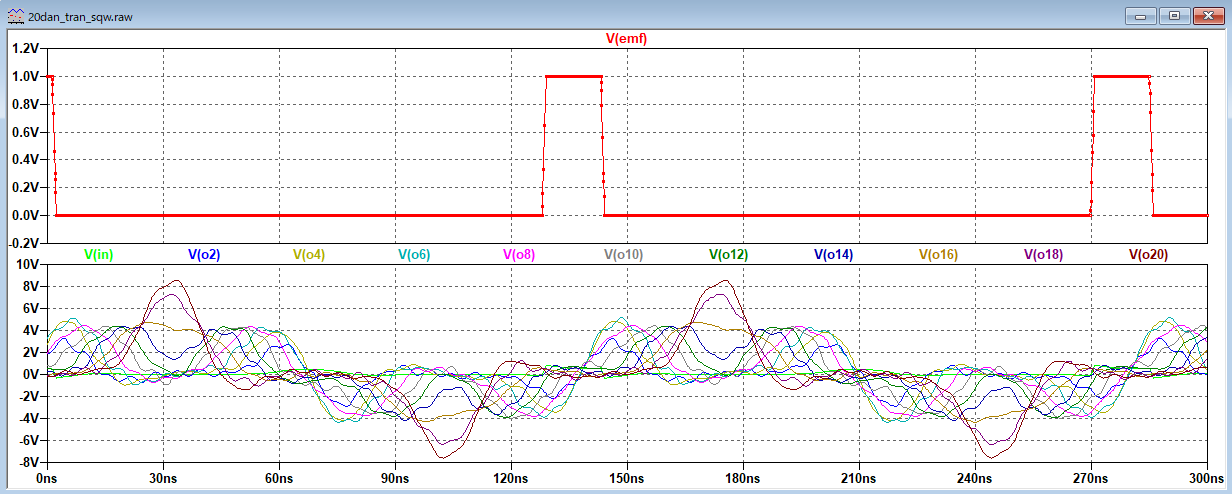
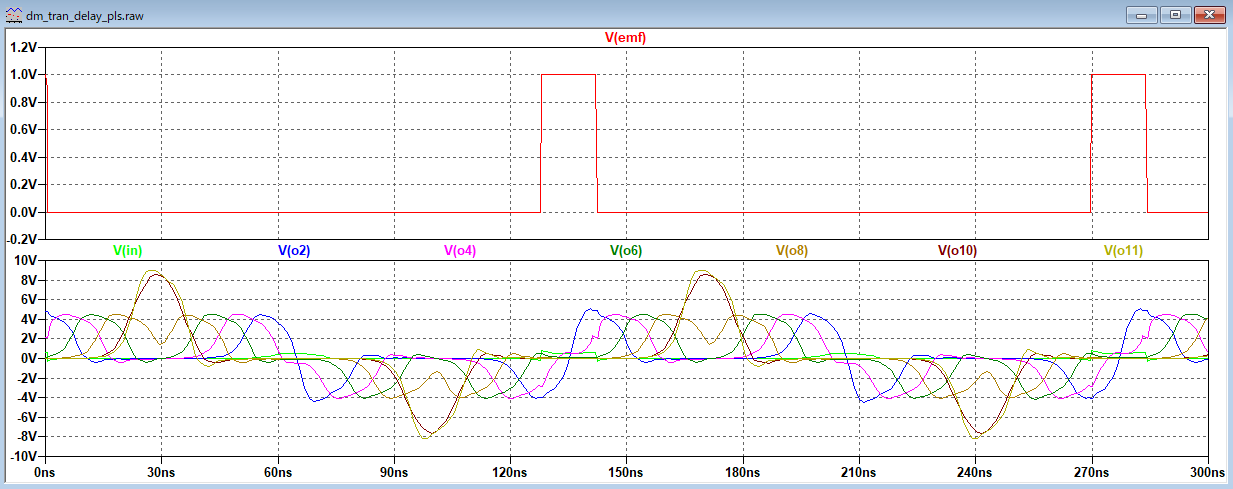
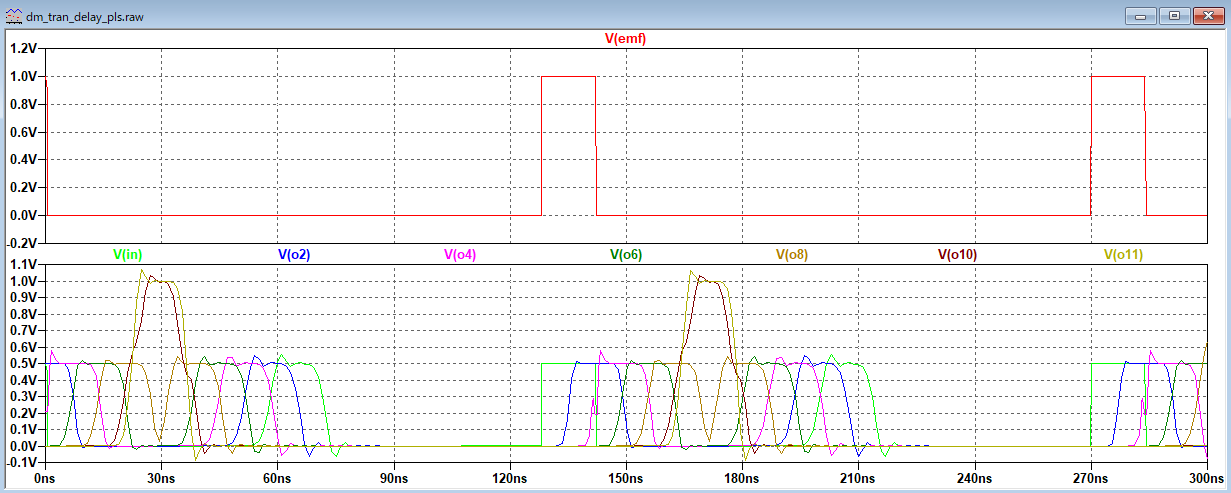
 適用例題1 キャパシタンスローディング
適用例題1 キャパシタンスローディング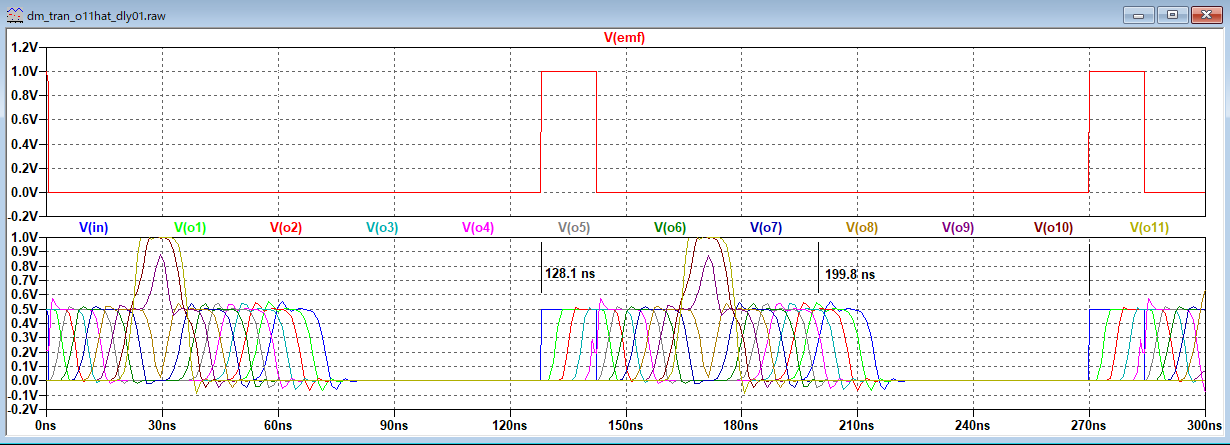
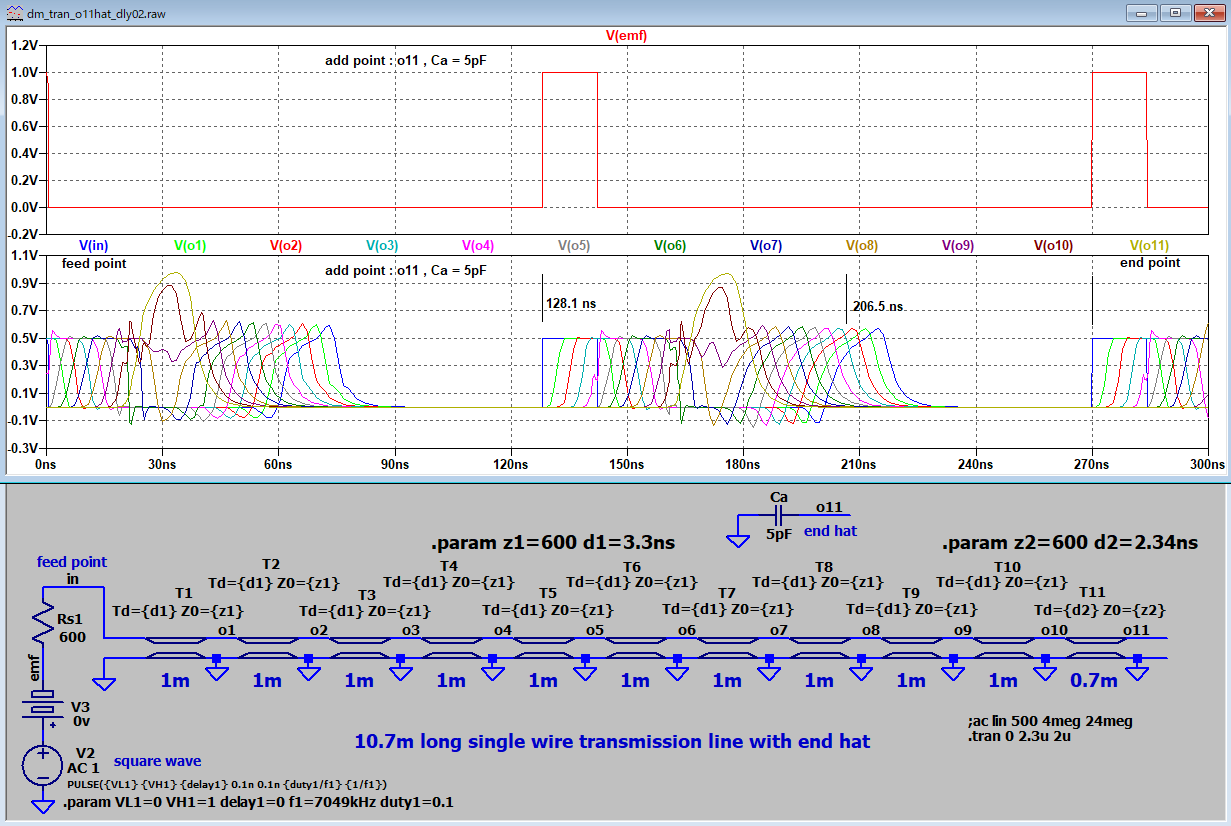
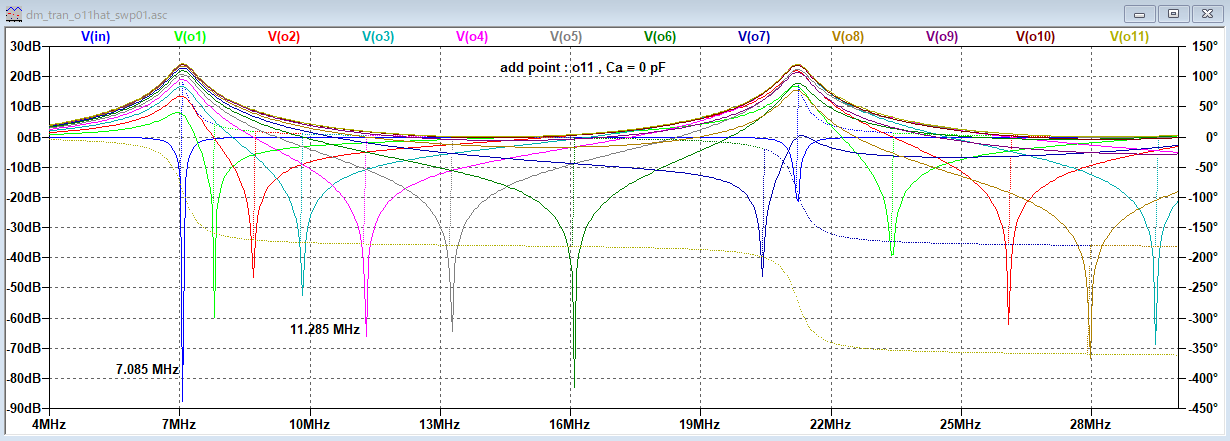
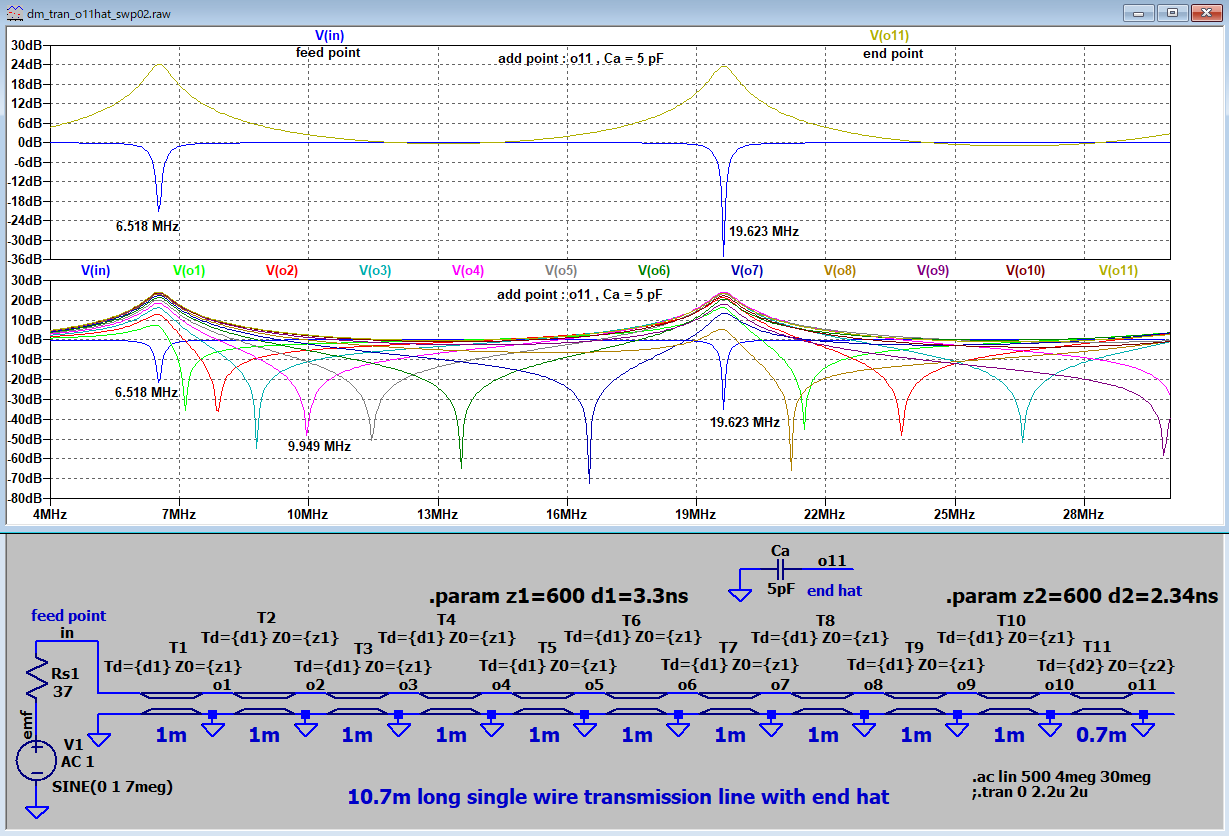
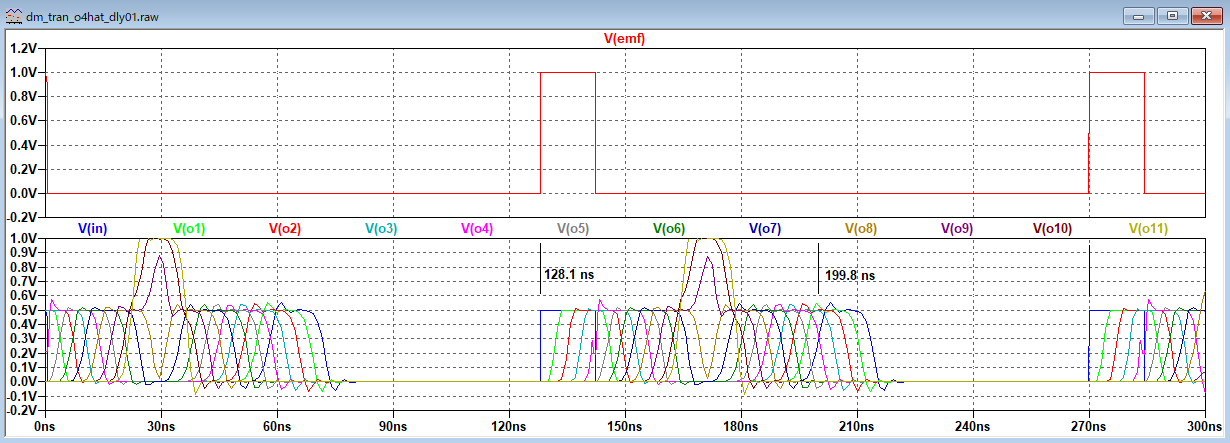
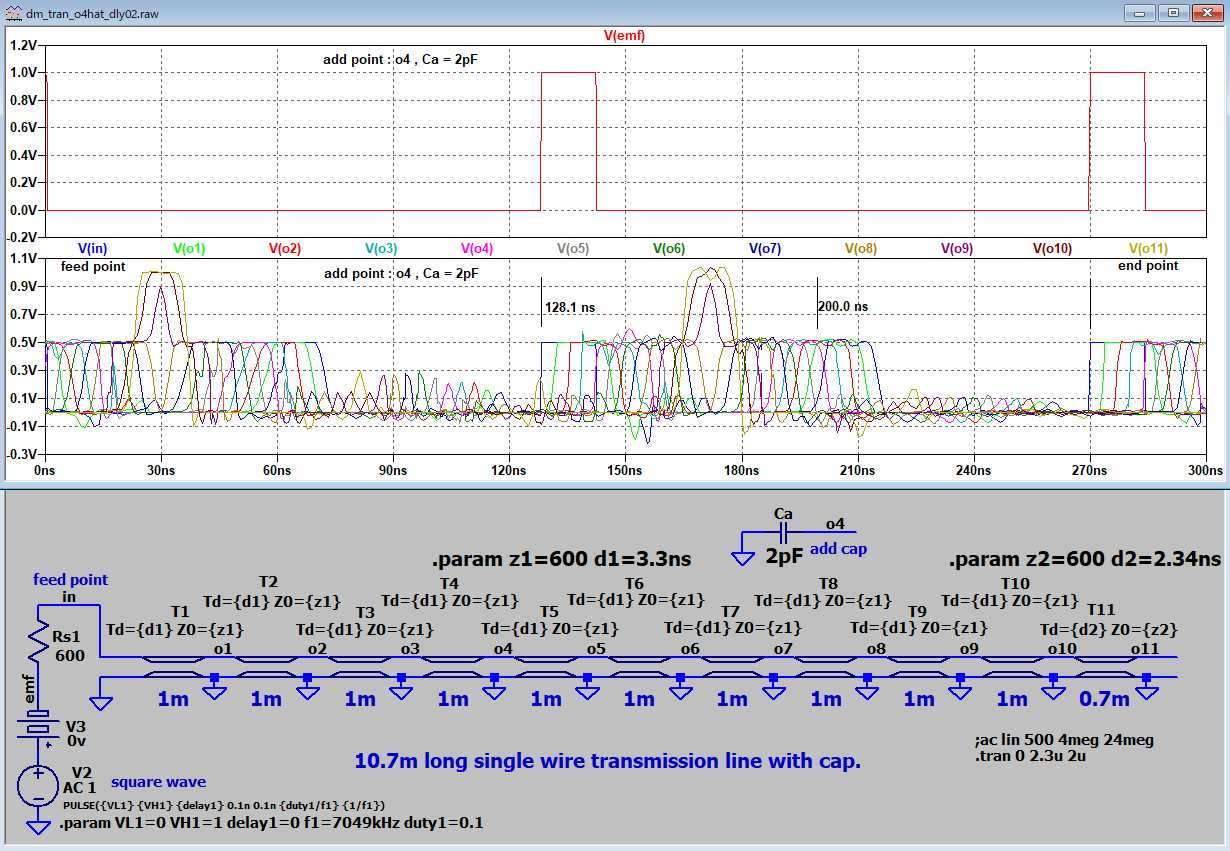
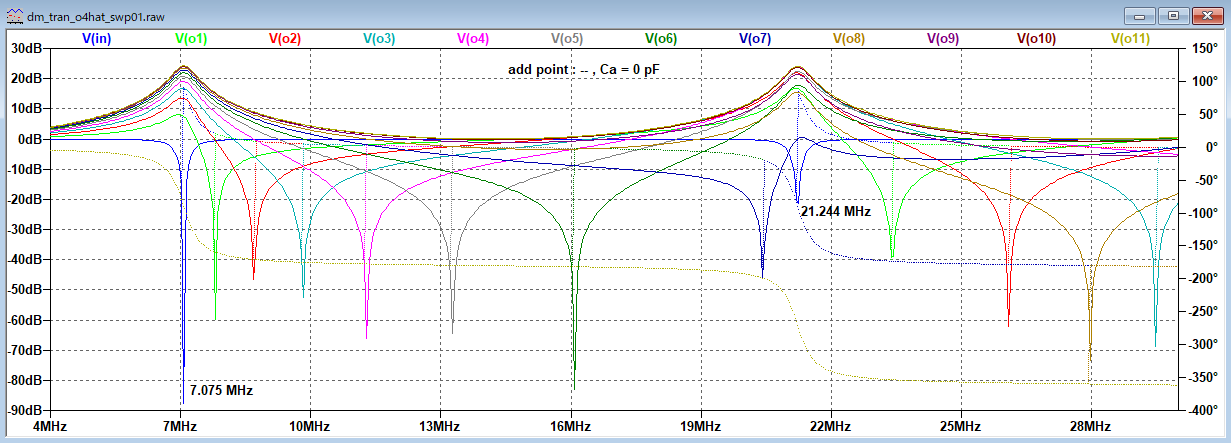
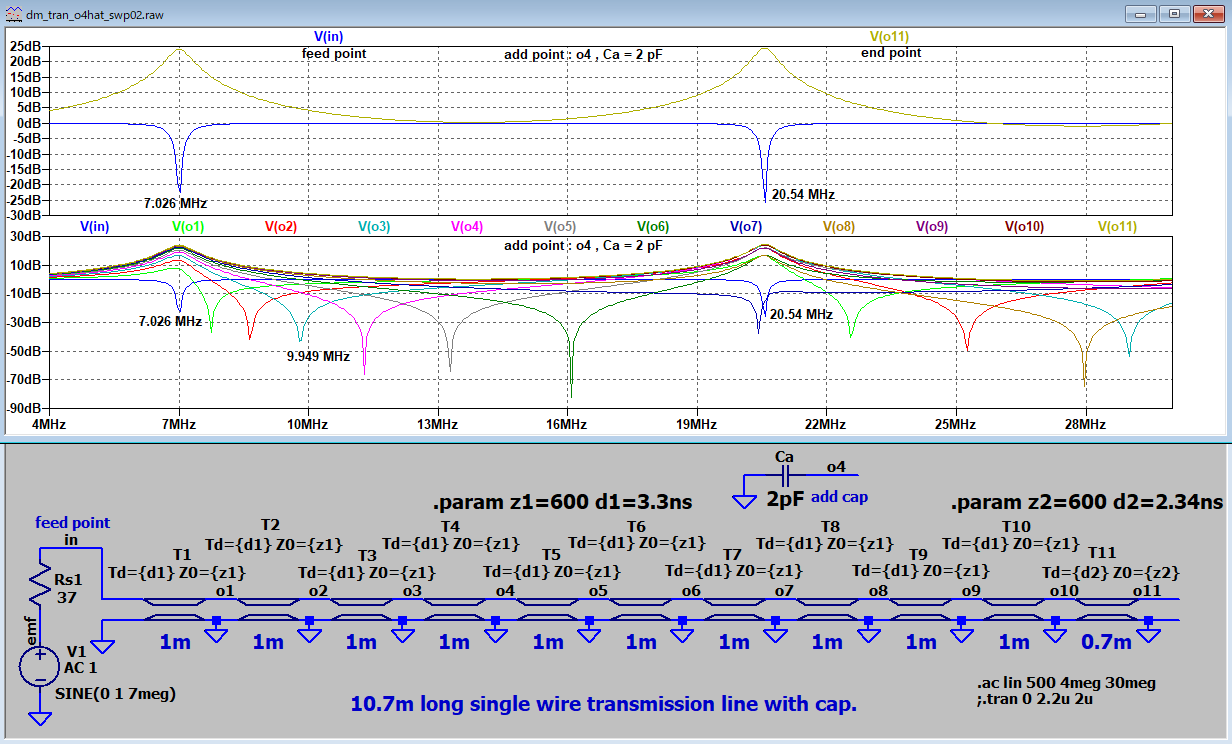
 適用例題2 インダクタンスローディング
適用例題2 インダクタンスローディング