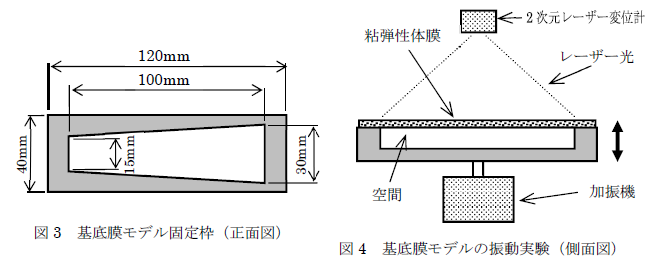
固定枠は剛性の高い塩ビ材によるもので供試体膜をこの面に張り付けます。振動入力は固定枠全体を加振し供試体面全体を振らせます。供試体膜表面での振動変位はレーザ変位計にて2次元計測されます。
| 聴覚歪とは | 歪が生じるメカニズム | 耳の構造とはたらき | 基底板による周波数弁別 | 外有毛細胞による再生増幅 |
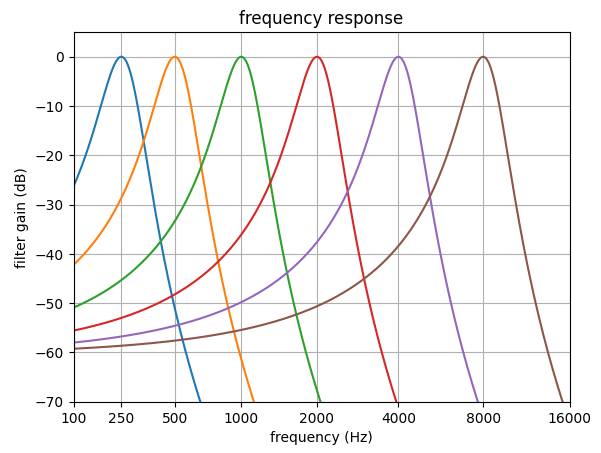
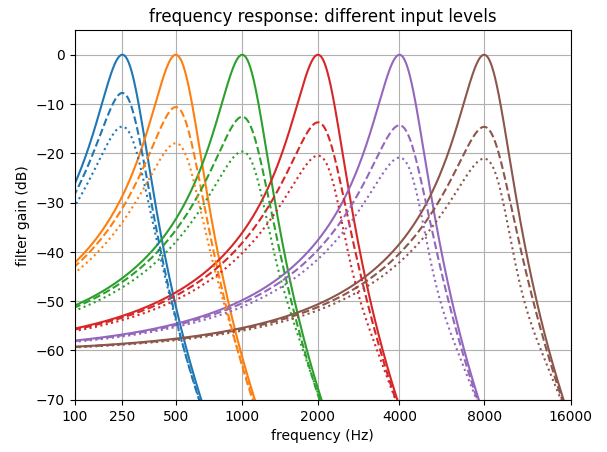
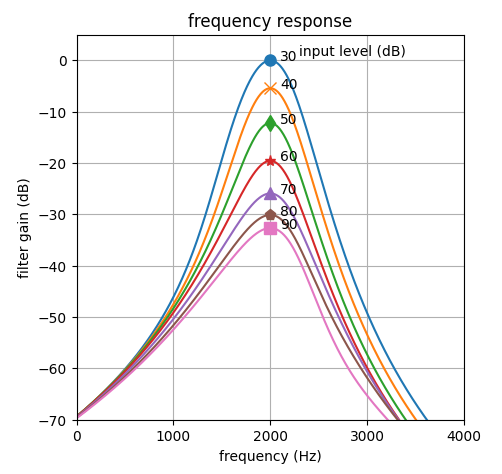
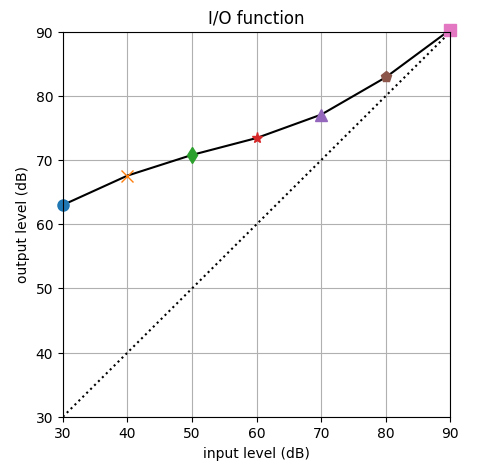
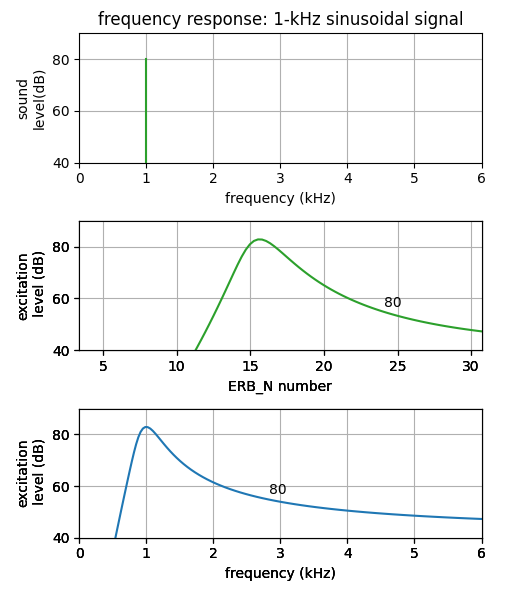
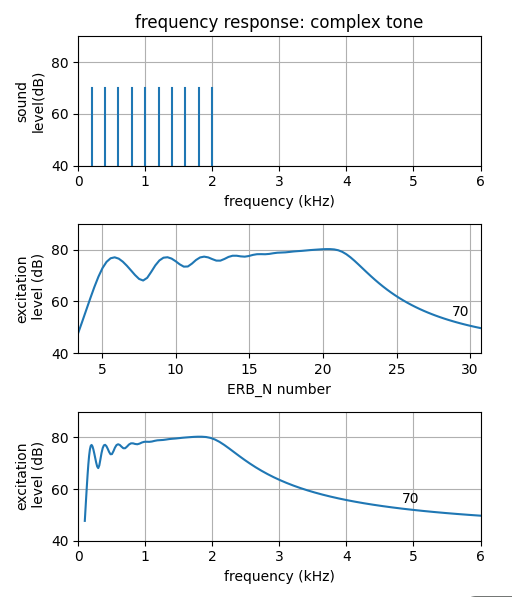
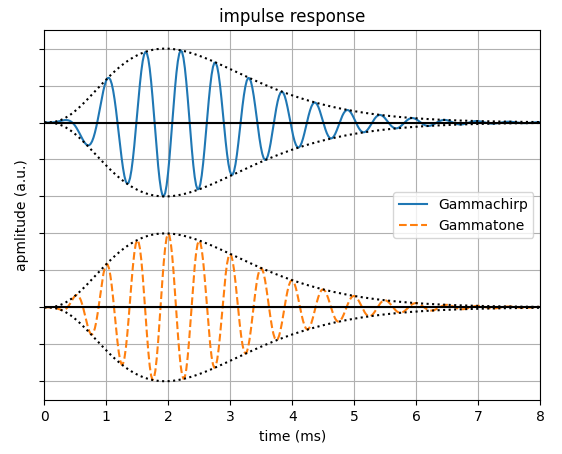
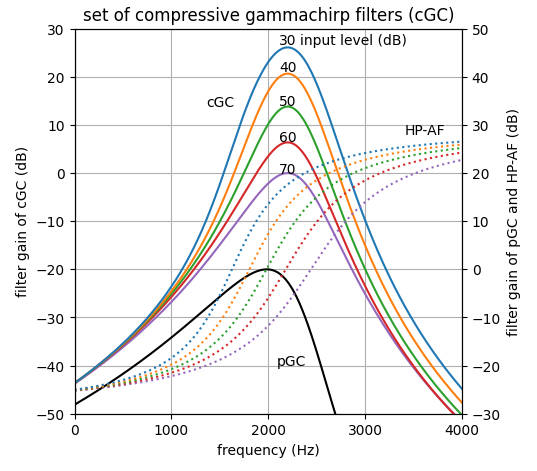
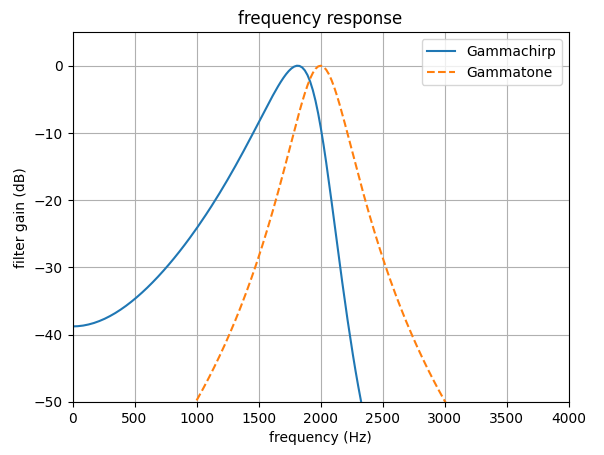
| 聴覚フィルタの概念 | <振幅周波数特性> | <音圧依存性> | <マスク信号による聴感刺激> | <インパルス応答> |
| <ガンマチャープフィルタの生成> |
 聴覚歪とは
聴覚歪とは 歪が生じるメカニズム
歪が生じるメカニズム 耳の構造とはたらき
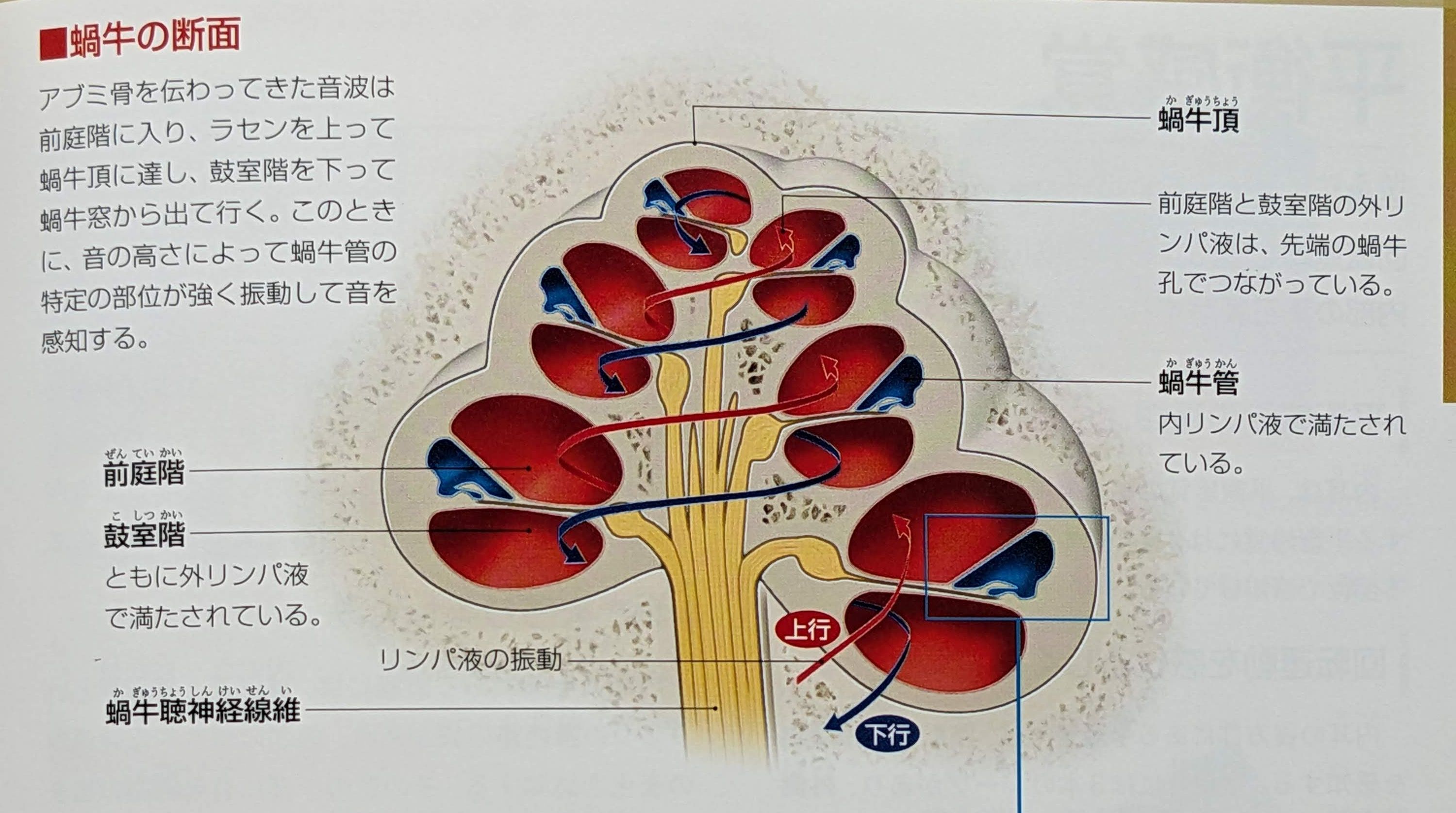
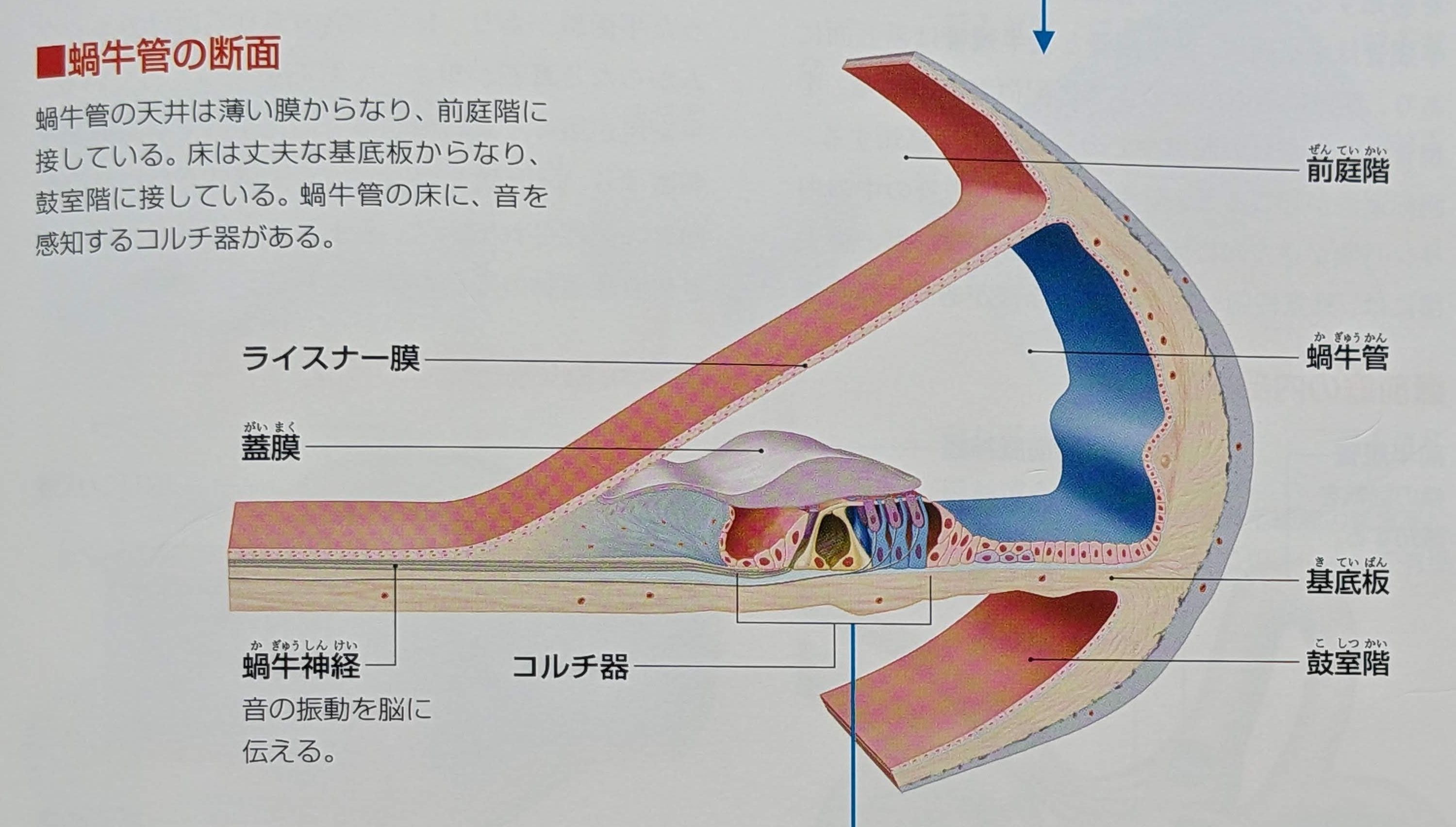
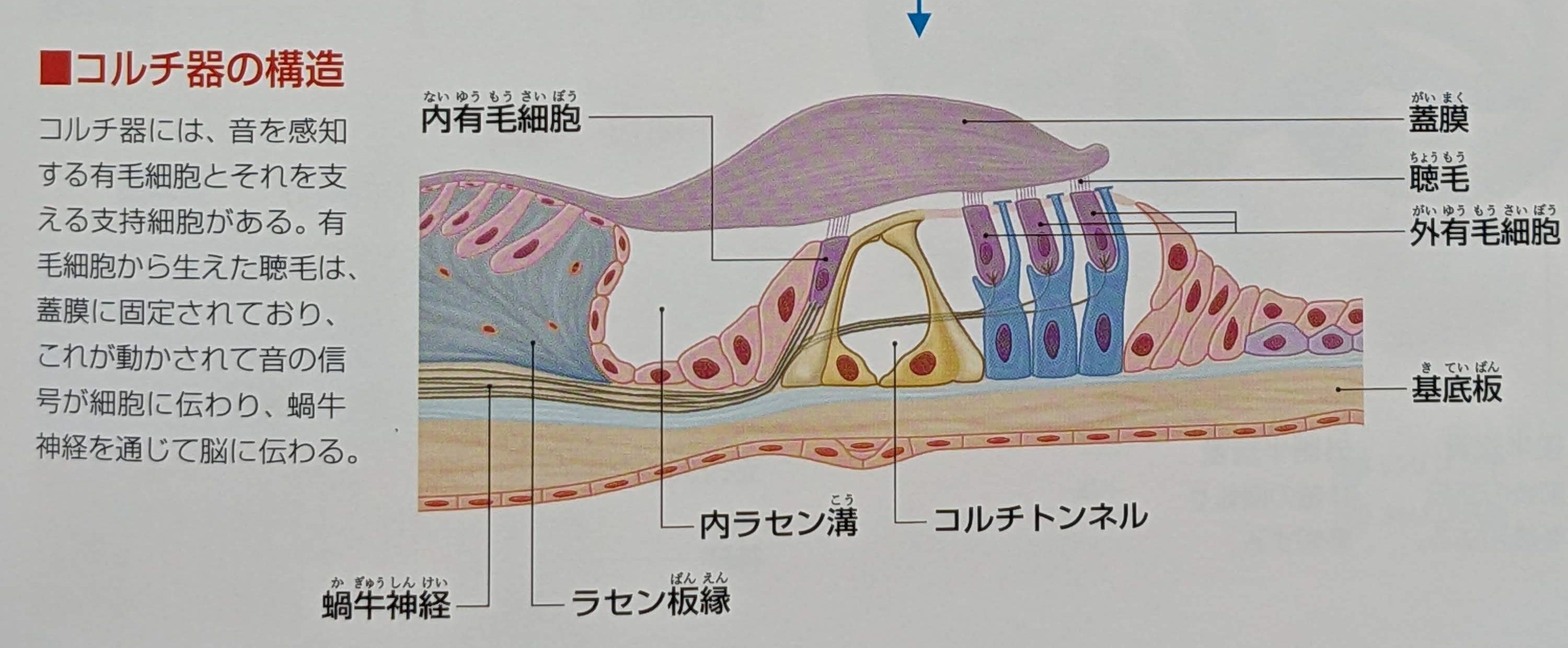
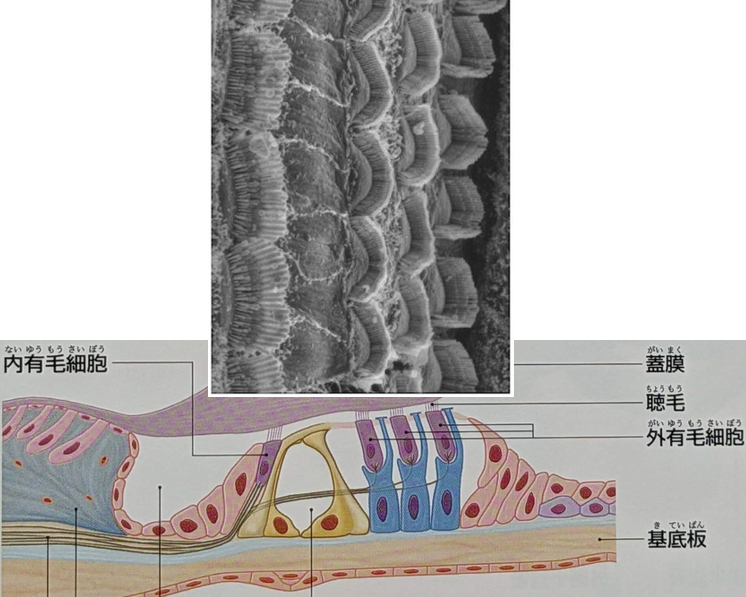
耳の構造とはたらき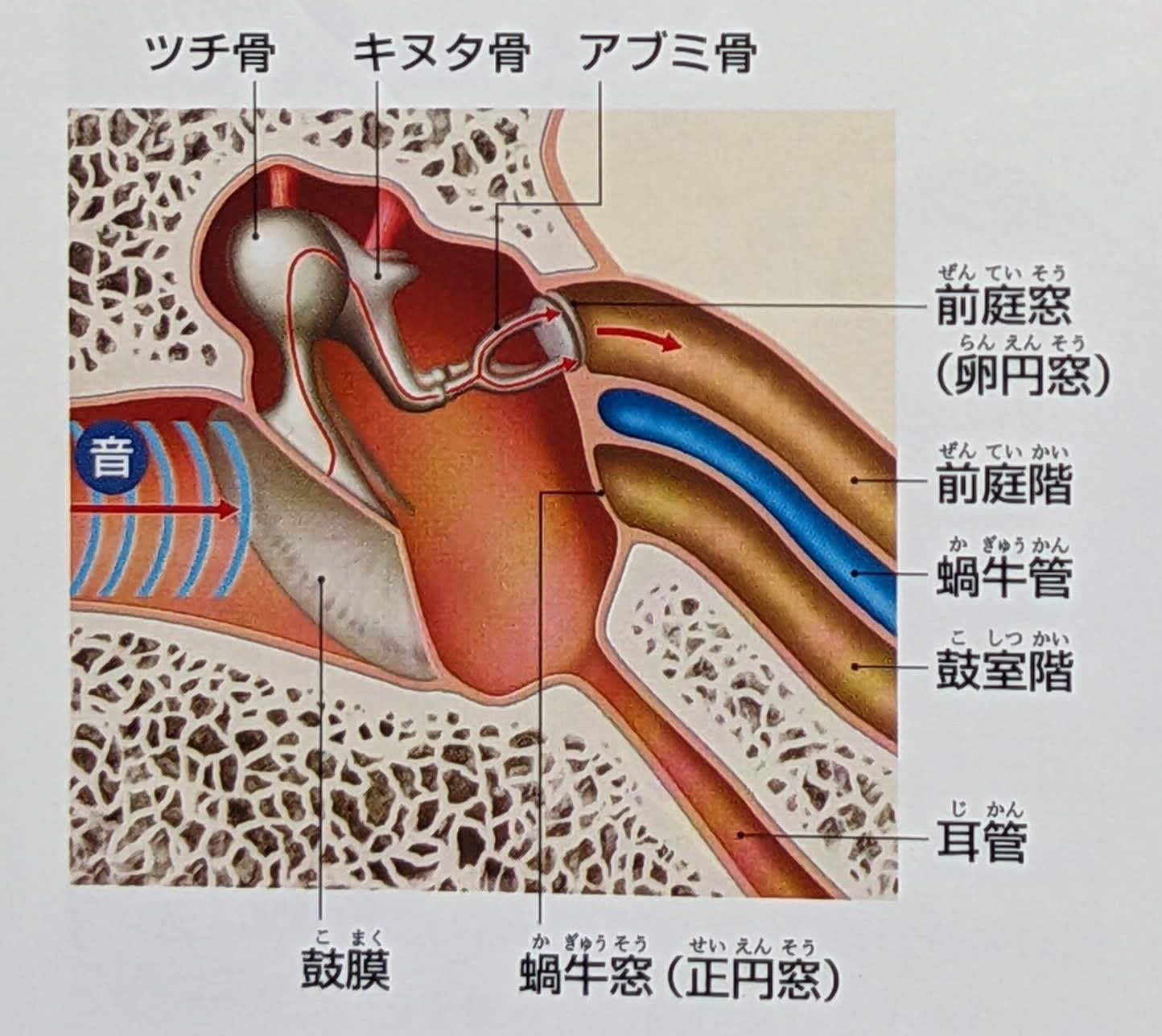
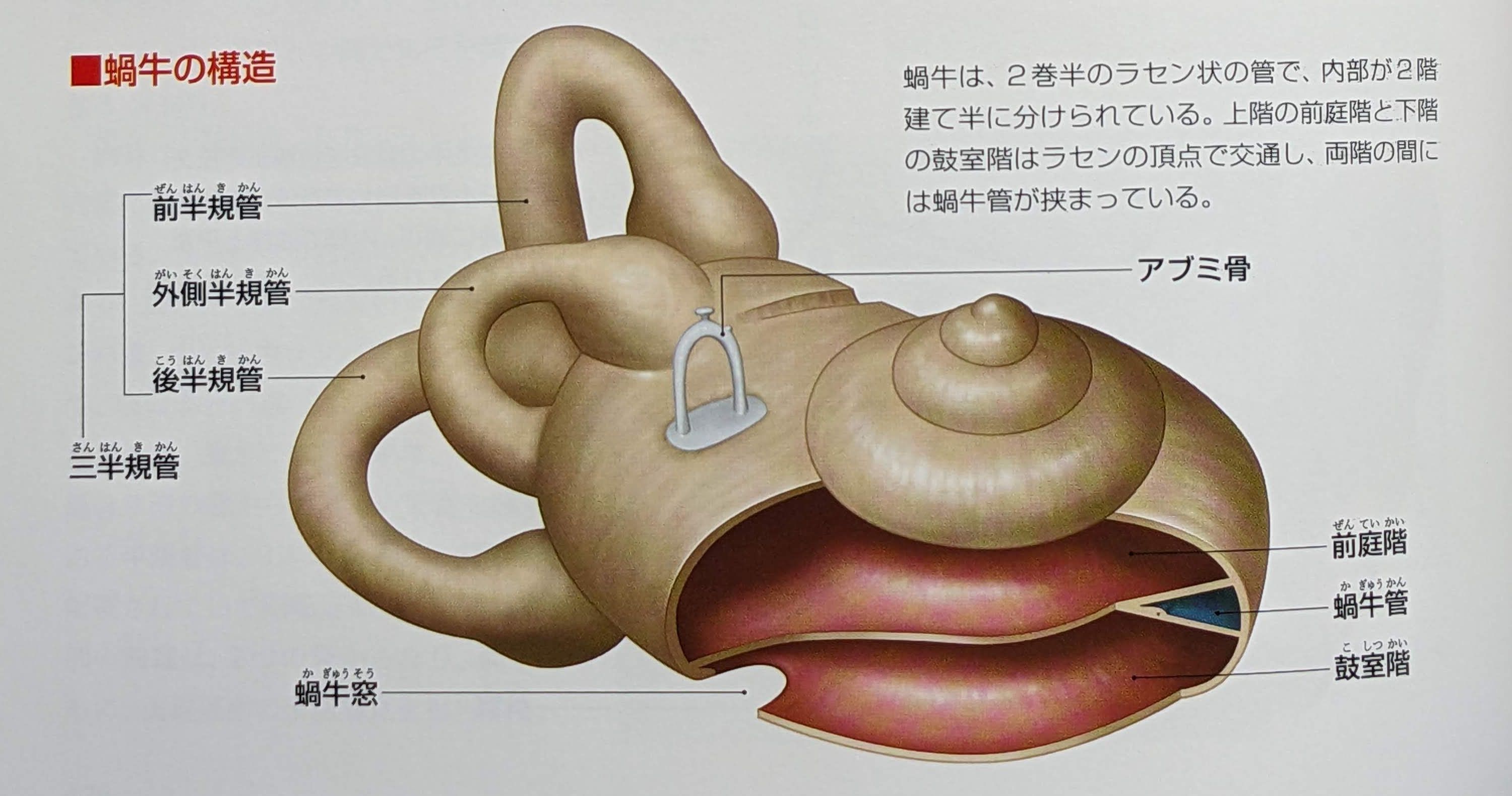
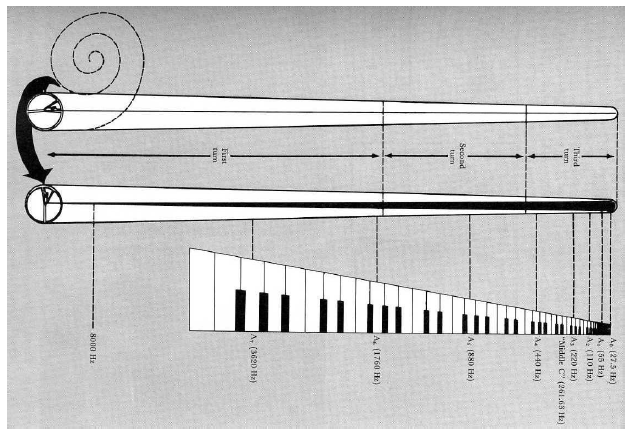
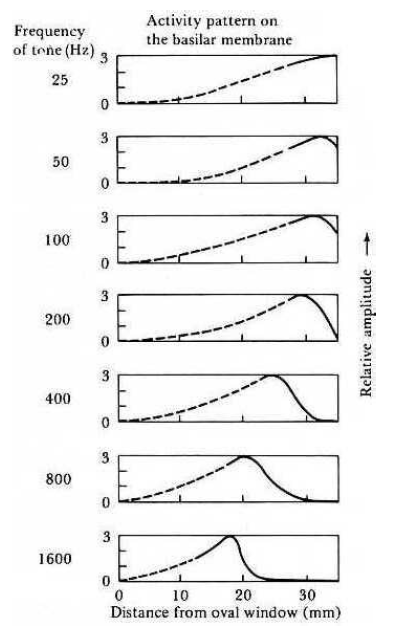
 基底板による周波数弁別
基底板による周波数弁別 |
固定枠は剛性の高い塩ビ材によるもので供試体膜をこの面に張り付けます。振動入力は固定枠全体を加振し供試体面全体を振らせます。供試体膜表面での振動変位はレーザ変位計にて2次元計測されます。 |
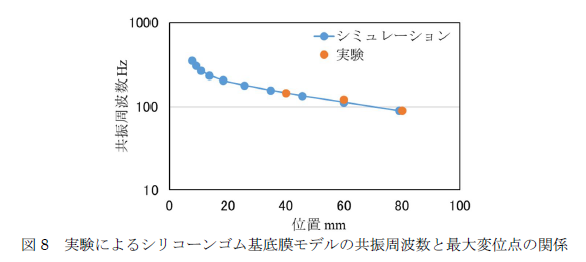 |
供試シリコンゴム膜の寸法形状・材料物性に沿った有限要素法解析(シミュレーション)と強制振動入力による実験計測結果です。なお点列を成す振動固有値は右台形長辺側から左台形短辺側に順に周波数・固有値次数が増えています。 |
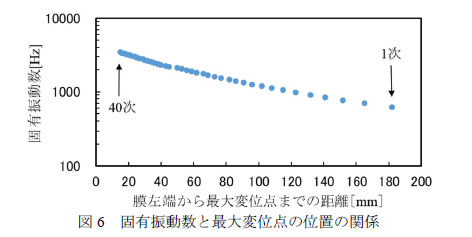 |
これは保持枠寸法、供試シリコンゴム膜寸法が上とは違いますが有限要素法解析(シミュレーション)で基本から40次までの高次固有値振幅最大位置が求められたものです。 |
 |  | |
 外有毛細胞による再生増幅
外有毛細胞による再生増幅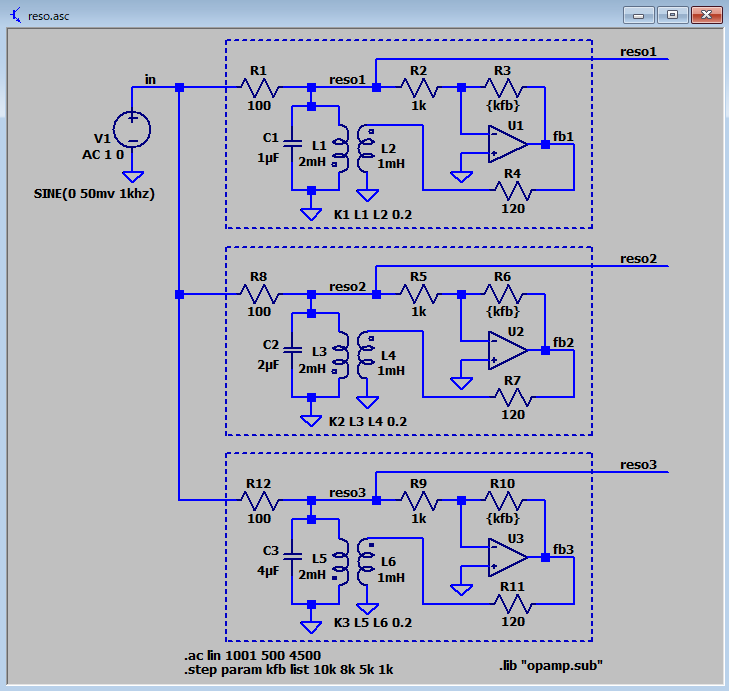
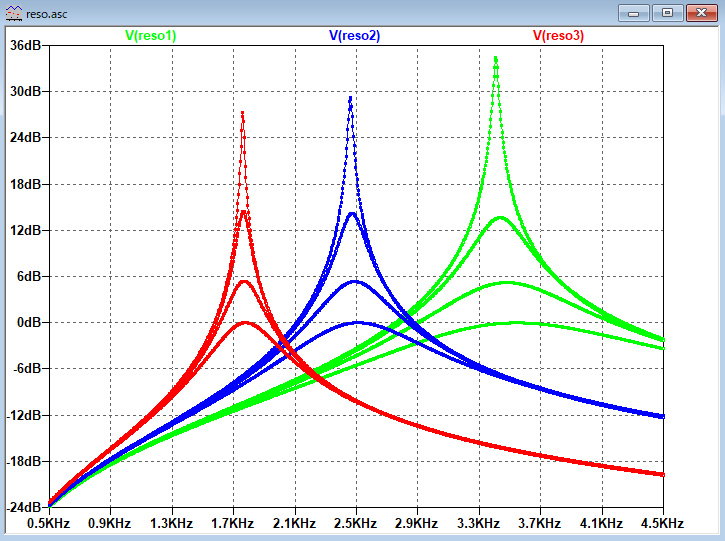
 聴覚フィルタの概念
聴覚フィルタの概念